

On May 13th 2025, I appeared for the research interview at the IISc computer science department. In this post, you can find my detailed interview experience and some preparation methods I used for my interview.
Background: After GATE 2025 results, IISc called for applications to research programmes. This includes two programmes: M.Tech research and PhD. The selection procedure happened together for both of them. On 16th April, I got the interview call letter, where they mentioned my interview date (May 13). A few days after that, the CS department circulated a Google form – where we need to select a research substream, two research subareas, and two background subjects. A table is attached below for reference:
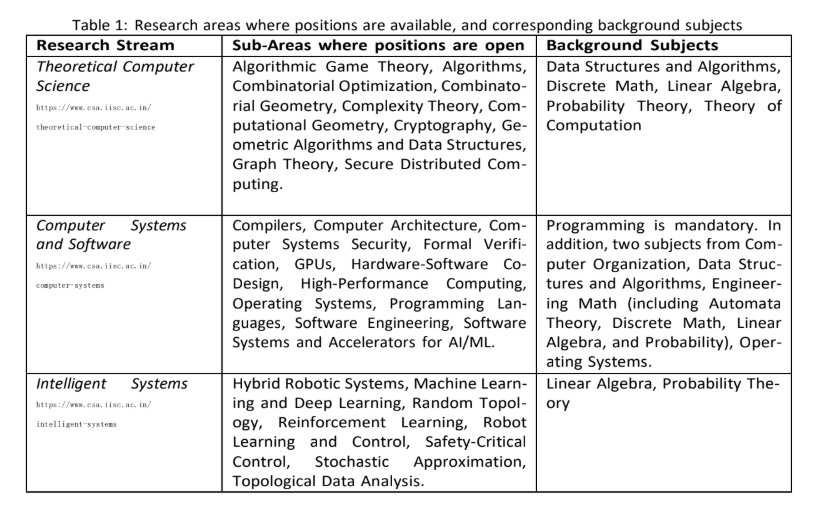
Please note that selection of substream is very important because you cannot change it once you are admitted to the programme. But selection of sub area and background subject is only for the purpose of interview. Since I'm a theory lover, I selected Theoretical computer science. I selected Combinatorics and Algorithms as my sub areas, Discrete math and Probability as my background subjects.
Interview experience : I reported to the CSA department at 8:45 in the morning. There were
around 25 students reported for that particular day. After some paperwork, the department fellows divided us
into different groups, where each group represents an interview panel which we are going to get. In our theory panel,
there were 5 students (all of us became friends that day :D ). At around 9:45, professors began to call us one by one,
in alphabetical order. Since I was last in that order, I had to wait for around 3 hours. After that long wait, my turn came.
I entered the room with a mind filled with anxious questions. It was like a small seminar room, where there was
a big whiteboard and a long table in front of it. My panellists were three professors – Prof. Sunil Chandran (graph theory),
Prof. Satish Govindarajan (computational geometry) and Prof. Arpita Patra (cryptography).
For simplicity, I will use P1, P2 and P3, respectively, for addressing them. :
P2 : read aloud my name,gate score, college etc.
Me: (Confirms it)
P2: “Can we start with Discrete math? Or do you want probability first?”
Me: “ I prefer Probability, sir”
P1 : (starts with a question)
“I give you a coin – when we toss it, the head appears with a probability of p. What is the expected number of tosses
we need to get the first head?”
( This is a very common GATE question, so I felt confident. But it's important to remember that, in research interviews,
whatever you say, you need to give proper proof/justification. A direct answer will never be appreciated.
So I started from fundamentals, explained the memorylessness property and drew a probability tree for the coin tossing experiment.
In the end, I derived the final answer = 1/p )
P1 : “Good. But I want a more straightforward solution – can you think of some other way?”
Me : (silently thinking)
P1 : “What is the random variable here?”
Me : (draws the graph of a single coin random variable and says that it's a Bernoulli random variable – but this was wrong
since the random variable in question was a different one)
P1 : “So you didn't understand the random variable in question properly. Then how did you get the
answer earlier?”
(At this point, I felt real pressure. But fortunately I kept my nerve and thought about the question.
Soon I got the right lead.)
Me : "Okay, now I understand my mistake, sir; it is a geometric random variable. I will derive this way”
(I drew the bar graph of that random variable and started finding the expectation by adding the infinite G.P. I used the formulae for
summation of infinite G.P., but right after the use, I derived the formula on the board as well, which impressed the professors.
I concluded the question with the right answer. )
P1 : “Very good. Now Let me ask a new question” (Thought for a while)
“There is a fixed graph G, which is simple and undirected. The only thing we know about this graph is that it has m edges.
Now you partition the vertices of this graph into two sets – set A and set B. For each vertex you will toss a fair coin:
if it turns up heads, you will put the vertex in set A. If it turns up tails, you will put that vertex in set B. So on.”
Me : (Comprehends the question in silence)
P1 : (continues) “Now there will be few edges going from set A to set B right? These edges are called -
cuts - What is the expected number of cuts for the given graph?”
Me : (I had no clue how to approach this question, but I started by representing the two sets on the board. Soon I realised that
the probability of an edge being a ‘cut’ is ½. From there I developed the solution and reached the final answer,
with a few helps from professors.)
P1 : “Very good. Now I will ask one last question; after that, it's over from my side.”
Me : “Okay” (I felt confident, as my first phase of interview went well)
P1 : “You have a set of k-dimensional vectors. Every entry to this column vector is either 0 or 1. The set contains all such
k-dimensional vectors.”
Me : “So for example, vectors like [ 0,0,0,....,0 ], [ 1,1,0,1,...] with k entries are present in the set.
Right?”
P1 : “Exactly. Now we represent each vector with a vertex of a simple graph. Two vertices are connected by an edge if and only
if the corresponding vectors differ exactly by 1 digit.”
Me : “So [0,0,0,....] is connected with all vectors with exactly one 1”
P1: “Yes. So the question is - how many edges will be there in this graph?”
Me : (I already have the lead, so I started with stating that each vertex has degree k. I found the total sum of degrees,
which is twice the number of edges. Stated the handshaking theorem and reached the final answer = (2^k) * k / 2)
P1 : (Looks impressed) “Very good.”
(Professors also asked from where I studied to approach discrete math like ‘this’. And some other similar questions – this obviously
boosted my confidence further.)
P2 : “Are you comfortable with Algorithms?” (He was asking that because I'm an ECE graduate)
Me : (It was not in the background subjects I selected, so it surprised me a bit)
“I had a course during my bachelors, but I don't remember the advanced concepts”
P2 : “That's fine, I will only ask one simple question from this” (and starts with the question)
“You are given an array of n distinct integers. An element in this array is a local maximum if it is greater than the elements
adjacent to it. Can you tell an algorithm to find whether local maximums exist or not?”
Me : “So is it like, the first element is a local maximum if it is greater than the second element?”
P2 : “Yes, correct”
Me : (After a brief thought, I understood a local maximum will exist no matter what. I used proof by contradiction to state that)
P2 : “Now a slight variation - I want you to report any local maximum. Tell me an algorithm”
Me : (I told linear scanning method)
P2 : "What is the time complexity of your algorithm?"
Me : “Order of n”
P2 : “Correct. Can we do this faster?”
Me : (Thought for a while, then went for a method which is like a binary search – the professor gave me enough hints here
so that I completed the algorithm.)
P2 : “Yeah, good. That's it”
(After this, all three professors asked some non-technical questions. Some questions were related to my future plans and all –
due to that, I had an intuition that I was getting selected. Once it was over, they told me I could leave.)
I left the room with a happy face. Roamed the beautiful campus for some time, ate mushroom fried rice from the canteen, called my parents –
and left the campus with a content heart.
Verdict : On May 30, CSA put out a provisional list of candidates who cleared the interview. My application number was in it. But this list only means we cleared the interview – only if we get the offer letter, admission will be confirmed. On June 2 in the evening, I got the offer letter – which starts with “Hearty Congratulations!” I was extremely happy for that entire week, so much so that my friend even started doubting whether I have madness or not :p
Take away for future aspirants : You may have observed the questions were asked from fundamental concepts. So whatever the topic you choose, stick to the fundamentals. Many basic concepts like random variables, degree of a graph, etc., are very easy to ignore. But when we try to define those terms without the help of a textbook, we will realise the loopholes in our understanding. So understand the basics well. Also go through past interview experiences (available in Gate Overflow). Previous questions may not repeat, but you can identify the types of questions they ask in research interviews. Finally, try to be calm on the interview day. This is very easy to say, but difficult to implement. I have a wall board in my study room, which I used frequently before the interview. This helped on the day of the interview, as I never felt anything unusual while doing problems on the board.

